Ecuación de Primer Grado

 

Resolver una Ecuación de Primer Grado

        Ecuación:

Es un enunciado que establece que dos expresiones son iguales, en ella incluyen términos conocidos, variables o incógnitas y signos de operación y agrupación.

Ejemplo 1:

Carolina tiene 6 años menos que su hermano José Luis. Si ambas edades suman 26 años, ¿cuál es la edad de cada uno?

1. Comprender el Problema:

    ¿Qué debo encontrar? la edad de Carolina y la edad de José Luis.

2. Formular un Plan:

Es un problema que se puede resolver aplicando la estrategia resolver una ecuación de primer grado, ya que la información nos dice Carolina + edad de José Luis = 26 años. Si llamamos X a la edad de Carolina, entonces como ella es menor en 6 años que su hermano la edad de este es X +  6 y tenemos la ecuación.

x + (x + 6)= 26

3. Llevar a Cabo el Plan:

x + (x + 6)= 26

x + x + 6 = 26

2x + 6 - 6 = 26 - 6

2x = 20

x = 20/2

x = 10

4. Revisar y Comprar:

Esta comprobación  se puede realizar sustituyendo la solución en la ecuación original  y verificando la igualdad.

x + (x + 6)= 26

10 + (10 + 6) = 26

10 + 16 = 26

26 = 26

Ejemplo 2:

Ejemplo 3:

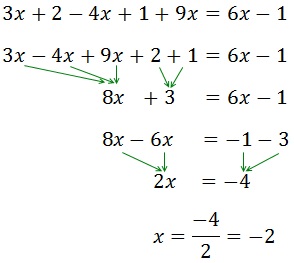
Comentario:

Las ecuaciones de primer grado, se me hacen difíciles al momento de tener que platear la ecuación  por medio de un problema dado, pero de lo contrario resolver una ecuación de primer grado es fácil, pero es difícil comprender cuando se tiene que hacer la transposición de términos, cuando se confunde al hacerlo que de más se pasa a menos etc.